Šiandien jau nieko nestebina tai, kad mokslininkai ir inžinieriai daugiau laiko praleidžia dirbdami asmeniniu kompiuteriu ar superkompiuteriu nei atlikdami natūrinius eksperimentus laboratorijose ar dalyvaudami teoriniuose seminaruose. Įprastiniais tapo tokie terminai, kaip „matematinis modeliavimas“, „virtualioji laboratorija“ ar „virtualusis eksperimentas“. Pasistengsime trumpai paaiškinti tas sąvokas. (Išsamias modeliavimo žinias ir įgūdžius suteikia studijų programa „Technomatematika“).

Pirmiausiai prisiminkime klasikinį žinių įgijimo būdą, nuo senų laikų taikomą ne tik universitetinėse studijose, bet ir kuriant bei naudojant naujas technologijas, gaminius ar paslaugas įvairiose gyvenimo srityse.

Taikant šį būdą, pavyzdžiui, inžinerijoje, laboratorijose atliekami eksperimentai, gauti rezultatai analizuojami, naudojant paprastus matematinius modelius, tų modelių taikymo rezultatų pagrindu formuluojamos naujos hipotezės, kurios vėl tikrinamos laboratorinių eksperimentų pagalba. Taip kaupiama patirtis ir žinios, kurių pagrindu gimsta naujos teorijos, leidžiančios kryptingai planuoti eksperimentus, paaiškinti jų rezultatus, iškelti naujus tikslus ir juos įgyvendinti. Toks ciklas kartojamas daug kartų, kol atsiranda naujas automobilis, lėktuvas, sukuriami nauji vaistai, pagaminamas televizorius ar radijo imtuvas. Tačiau toks kelias yra ne tik ilgas ir brangus, bet jo taikymo ribos tampa stabdžiu plėtojant naujas technologijas. Pavyzdžiui, kaip atlikti eksperimentus, kai reikia nagrinėti nanometrų dydžio daleles, kaip įvertinti šviesos greičiu judančio lazerio spindulio savybes?

Įveikti šias problemas padeda matematiniai modeliai ir kompiuterinės technikos galimybės.

Šiuolaikinio matematinio modeliavimo metodologijos esmė yra tiriamo realaus objekto (proceso, reiškinio, sistemos) pakeitimas jo „atvaizdu“ – matematiniu modeliu, o vėliau – virtualiuoju objektu (matematinio modelio kompiuterine realizacija). Tokiu būdu žymi dalis realaus objekto savybių tyrimo atliekama eksperimentuojant su virtualiuoju objektu. Šis trečiasis pažinimo (progozavimo, projektavimo) metodas turi savyje daugelį gerų pirmųjų dviejų mokslinio tyrimo metodų – teorijos ir eksperimento savybių. Darbas ne su pačiu realiuoju objektu, o su jo modeliu leidžia be didelių išlaidų ir pakankamai greitai atlikti jo savybių ir elgesio tyrimą įvairiausiose įmanomose situacijose (teorijos privalumai). Tuo pat metu skaitiniai (kompiuteriniai, simuliaciniai, imitaciniai) eksperimentai su objektų modeliais leidžia remiantis šiuolaikinių skaitinių metodų ir informatikos techninių priemonių galia detaliai, giliai ir pakankamai pilnai ištirti objektus, ką ne visada leidžia grynai teoriniai metodai (eksperimento privalumai).

Šią metodologiją taikant praktikoje paprastai tenka praeiti kelis tyrimo etapus. Tai galima pailiustruoti tokia schema:
 

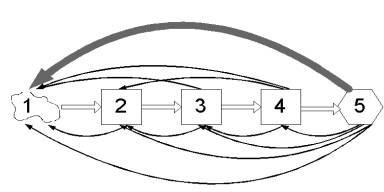Šioje schemoje skaičiais pažymėti:   1 – realusis objektas,   2 – idealizuota schema,   3 – matematinis modelis,   4 – skaitinis modelis ir jį realizuojantys algoritmai,   5 – virtualusis objektas.

Dvigubomis rodyklėmis pažymėti perėjimai tarp nuoseklių tyrimo etapų, viengubomis – grįžimas į ankstesnius etapus (tai neišvengiama dėl tobulėjančios kompiuterinės technikos, besiplėtojančių matematikos ir kitų mokslų metodų, o taip pat galimų klaidų ir netikslumų bet kuriame etape). Plati juoda rodyklė vaizduoja virtualaus objekto tyrimo rezultatų panaudojimą realiojo objekto pažinimui (struktūros ir funkcijų analizei), prognozei, projektavimui ir valdymui.

Matome, kad kompiuterinio modeliavimo bendroji schema yra panaši į klasikinės tyrimų metodologijos schemą, tačiau čia galime pastebėti kelis svarbius skirtumus:

    a) galime nagrinėti labai sudėtingus matematinius modelius. Jų sudarymas ir naudojimas yra kertinė viso kompiuterinio modeliavimo dalis. Šiuo metu jau sukurta daug metodų, leidžiančių aprašyti diferencialinėmis, integralinėmis ir kitokiomis lygtimis daugelį mus dominančių procesų gamtos, technologijos ar socialiniuose moksluose. (Studijuodami mūsų programoje išmoksite tokius modelius sudaryti, juos programiškai realizuoti ir analizuoti skaičiavimų rezultatus);

   b) gautus matematinius uždavinius pakeičiame jų artiniais (kadangi neįmanoma jų išspręsti tiesiogiai, analiziškai). Šiuolaikiniais kompiuteriais tuos matematinių modelių artinius (diskrečiuosius analogus) jau galima apdoroti. Po skaičiavimo rezultatų vizualizavimo kompiuterio ekrane galime stebėti fantastiškiausius procesus, realiai vykstančius labai greitai, labai nutolusius, labai mažoje srityje ar tiesiog pavojingus ar neįmanomus įgyvendinti natūrinio eksperimento sąlygomis.

Atlikdami skaičiavimus kartais gauname šimtus gigabaitų duomenų. Juos analizuoti, rasti tarp jų vertingą informaciją vėlgi padeda kompiuteriai. Tai jau minėtos vizualizavimo galimybės bei statistinė analizė.

Jei prieš 50-100 metu mokslo ir technikos pasiekimų skatinamas visuomenės materialinės kultūros progresas labiausiai priklausė nuo energetinių resursų, tai šiuo metu svarbiausiu resursu tampa kompiuterių pajėgumas.

Nors asmeninių kompiuterių ir darbo stočių pajėgumai auga labai greitai (procesorių greitis padvigubėja maždaug kas 18 mėnesių), bet greitaeigiškumo poreikis auga žymiai greičiau. Todėl labai svarbu išmokti naudotis superkompiuteriais, lygiagrečiaisiais kompiuteriais ir pačiu didžiausiu pasaulyje kompiuteriu – globaliuoju Internet tinklu, jungiančiu milijonus kompiuterių.

Sėkmingą darbą techninių sistemų ir technologinių procesų modeliavimo srityje gali užtikrinti tiktai pakankamai aukšta kvalifikacija trijose srityse: matematikoje, informatikoje ir inžinerijoje. Technomatematika, kaip tai matyti iš mūsų emblemos, yra šių trijų sričių sankirtoje. Jos studijų programa yra gerai subalansuota minėtų sričių dalykų atžvilgiu, vykdoma aukštos kvalifikacijos dėstytojų, gerai aprūpinta materialiai, todėl studentams yra visos galimybės įgyti šiuolaikinę, turinčią dideles perspektyvas specialybę.